JEE 2017 :: Advanced 2017 :: Physics 2017

• Advanced 2017 - Physics 2017
• Advanced 2017 - Chemistry 2017
• Advanced 2017 - Mathematics 2017

A point charge +Q  is placed just outside an imaginary hemispherical surface of radius R as shown in the figure. Which of the following statement is/are correct?

Answer:

Explanation:

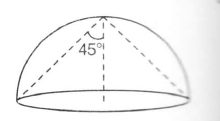
Ω = $2\pi(1-\cos\theta):\theta=$45° 

  $\phi =\frac{Ω}{4\pi}\times \frac{Q}{\epsilon_{0}}=-\frac{2\pi(1-\cos\theta)}{4\pi}\frac{Q}{\epsilon_{0}}$

= $=-\frac{Q}{2\epsilon_{0}}(1-\frac{1}{\sqrt{2}})$

(b)

   The component of the electric field perpendicular to the flat surface will decrease so we move away from the centre as the distance increases.

   (magnitude of electric field decreases) as well as the angle between the normal and electric field will increase. Hence, the component of the electric field normal to the flat surface is not constant.

ALTERNATE SOLUTION

     $x=\frac{R}{cos\theta}$

$E=\frac{KQ}{x^{2}}=\frac{KQ\cos^{2}\theta}{R^{2}}$

$\Rightarrow$   $E_{\perp}=\frac{KQ\cos^{3}\theta}{R^{2}}$

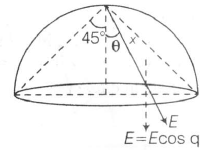
As we move away from centre

$\theta\uparrow\cos\theta\downarrow so E_{\perp}\downarrow$

(c)   Total flux Φ due to the charge Q is  $\frac{Q}{\epsilon_{0}}$

So, Φ through the curved and flux will be less than  $\frac{Q}{\epsilon_{0}}$

(d)   Since, the circumference is equidistant from Q it will be equipotential   $V= \frac{KQ}{\sqrt{2}R}$

A rocket is launched normal to the surface of the earth, away from the sun, along the line joining the sun and the earth. The sun 3× 10⁵ times heavier than the earth and is at a distance 2.5×10⁴ times larger than the radius of the earth. The escape velocity from the earth's gravitational field is V_e=11.2 km s^-1. The minimum initial velocity (V_s) required  for the rocket to be able to leave the sun-earth system is closest to (Ignore the rotation and revolution of the earth and the presence of any other planet)

Answer:

Explanation:

Given V_e= 11.2 km/s = $\sqrt{\frac{2GM_{e}}{R_{e}}}$

From energy conservation

                            K_i+U_i=K_f+U_f

$\frac{1}{2}mv_s^2-\frac{GM_{s}m}{r}-\frac{GM_{e}m}{R_{e}}=0+0$

Here r= distance of rocket from the sun

$\Rightarrow$     $                           V_{s}=\sqrt{\frac{2GM_{e}}{R_{e}}+\frac{2GM_{s}}{r}}$

  Given M_s  = 3× 10⁵ M_e

and r=2.5× 10⁴   R_e

$\Rightarrow$    $ V_{s}=\sqrt{\frac{2GM_{e}}{R_{e}}+(2G)(\frac{3\times 10^{5}M_{e}}{2.5\times 10^{4}R_{e}})}$

                          =$\sqrt{\frac{2GM_{e}}{R_{e}}(1+\frac{3\times 10^{5}}{2.5\times 10^{4}})}$

    =  $\sqrt{\frac{2GM_{e}}{R_{e}}\times 13}$

    = 42 km/s

A person measures the depth of a well by measuring the time interval between dropping a stone and receiving the sound of impact with the bottom of the well. The error in his measurement of time is $\delta T= 0.01s$  and he measures the depth of the well to be  L=20 m. Take the acceleration due to gravity g=10 ms^-2 and the velocity of sound is 300 ms^-1. Then the fractional error in the measurement

$\frac{\delta L}{L}$is closet to

Answer:

Explanation:

$t=\sqrt{\frac{L}{5}}+\frac{L}{300}$

$dt=\frac{1}{\sqrt{5}}\frac{1}{2}L^{-\frac{1}{2}}dL+(\frac{1}{300}dL)$

$dt=\frac{1}{2\sqrt{5}}\frac{1}{20}dL+\frac{dL}{300}=0.01$

  $dL(\frac{1}{20}+\frac{1}{300})=0.01$

       $dL(\frac{15}{300})=0.01$

       $dL=\frac{3}{16}$

$\frac{dL}{L}\times100=\frac{3}{16}\times\frac{1}{20}\times 100=\frac{15}{16}=1$%

Three vectors P, Q, and R  are shown in the figure. Let S be any point on the vector R. The distance between the point  P and S  is b[R]. The general relation among vectors P, Q and S is

Answer:

Explanation:

A photoelectric  material having work-function Φ₀ is illuminated with light of wavelength λ  $(\lambda <\frac{hc}{\phi_{0}})$ . The fastest photoelectron has de-Broglie wavelength λ_d. A change in wavelength of the incident light by Δλ results in a change Δλ_d in λ_d

Then, the ratio $\frac{\triangle \lambda_{d}}{\triangle\lambda}$ is proportional to

Answer:

Explanation:

According to photoelectric effect equation

$KE_{max}=\frac{hc}{\lambda}-\phi_{0}$

$\frac{p^{2}}{2m}=\frac{hc}{\lambda}-\phi_{0}$

                                                            [KE= P²/2m]

$\frac {\left(\frac{h}{\lambda_{d}}\right)^{2}}{2m}=\frac{hc}{\lambda}-\phi_{0}$

Assuming small changes, differentiates in both sides

$\frac{h^{2}}{2m}(-\frac{2d\lambda_{d}}{\lambda_d^3})=-\frac{hc}{\lambda^{2}} d\lambda$

$\frac{d\lambda_{d}}{d\lambda}\alpha \frac{\lambda_d^3}{\lambda^{2}}$

• Advanced 2017 - Physics 2017
• Advanced 2017 - Chemistry 2017
• Advanced 2017 - Mathematics 2017